روش مسیر بحرانی (Critical Path Method) چیست؟

الفبای روش مسیر بحرانی (Critical Path Method)

روش مسیر بحرانی (Critical Path Method) یک تکنیک قدرتمند اما ساده برای تحلیل، برنامه‌ریزی و زمانبندی پروژه‌های بزرگ و پیچیده است.

در اصل، این ابزار وسیله‌ای است برای تعیین اینکه کدام یک از فعالیت‌های پروژه‌، از نظر تأثیر بر زمان کل پروژه بحرانی هستند. همچنین به برنامه‌ریزی بهینه همه فعالیت‌های پروژه به منظور تحویل پروژه در تاریخ مورد نظر و با حداقل هزینه کمک می‌کند.

روش مسیر بحرانی (Critical Path Method) چیست؟

مفهوم روش مسیر بحرانی (Critical Path Method) ساده است و به بهترین شکل از طریق نمودار پروژه نشان داده می‌شود. نمودار پروژه برای به تصویر کشیدن بصری و واضح مجموعه فعالیت‌های یک پروژه و روابط متقابل آنها ارزشمند است. البته برنامه‌های کامپیوتری محاسبات لازم را بدون نیاز به نمودار انجام می‌دهند.

برای رسیدن به مسیر بحرانی:

1. فعالیت‌های لازم برای تکمیل یک پروژه هر یک با یک نماد شناسایی منحصر به فرد (مانند یک حرف یا شماره) به همراه زمان مورد نیاز برای تکمیل آنها و فعالیت‌های پیش‌نیازشان لیست می‌شوند. برای سهولت در رسم نمودار، فعالیت‌ها به ترتیب تکنولوژیکی مرتب شوند، به این معنی که تا زمانی که همه پیش‌نیازهای یک فعالیت فهرست نشده‌اند، آن فعالیت در لیست ظاهر نمی‌شود.
2. سپس هر فعالیت همراه با نماد شناسایی آن به صورت یک دایره بر روی نمودار کشیده می‌شود و زمان در داخل دایره قرار می‌گیرد. روابط توالی با فلش‌هایی که هر دایره (فعالیت) را به فعالیت‌های پسین آن متصل می‌کند، نشان داده می‌شود.
3. برای سهولت، همه حلقه‌های بدون پیش‌نیاز به حلقه‌ای با علامت شروع متصل می‌شوند. به همین ترتیب، همه حلقه‌های بدون فعالیت پسین به حلقه‌ای با علامت پایان متصل می‌شوند.
4. نمودار مسیرهای مختلف شروع تا پایان را نشان می‌دهد. زمان لازم برای پیمایش هر مسیر، مجموع زمان‌های مرتبط با تمام فعالیت‌های موجود در مسیر است. مسیر بحرانی (یا مسیرها) طولانی‌ترین مسیر زمانی از شروع تا پایان است.

مسیر بحرانی طولانی‌ترین مسیر زمانی از شروع تا پایان است.

در اصل، مسیر بحرانی گلوگاه پروژه است:

تنها با یافتن راه‌هایی برای کوتاه کردن فعالیت‌های موجود در مسیر بحرانی می‌توان زمان کلی پروژه را کاهش داد. زمان مورد نیاز برای انجام کارهای غیر بحرانی ارتباطی به زمان کل پروژه ندارد و عجله در انجام کارهای غیربحرانی برای کوتاه شدن زمان کل پروژه بی‌فایده است.

 به طور معمول، تنها حدود ۱۰ درصد از فعالیت‌های پروژه‌های بزرگ بحرانی هستند. (این رقم از پروژه‌ای به پروژه دیگر متفاوت خواهد بود.) البته، اگر راهی برای کوتاه کردن یک یا چند فعالیت بحرانی پیدا شود، نه تنها زمان کل پروژه کوتاه می‌شود، بلکه مسیر بحرانی نیز ممکن است تغییر کند و برخی از وظایف که سابقا غیر بحرانی بودند، بحرانی شوند.

مثال برای روش مسیر بحرانی (Critical Path Method): ساختن خانه

پروژه ساخت خانه به آسانی با تکنیک روش مسیر بحرانی (CPM) تحلیل می‌شود. لیست فعالیت‌های اصلی (همراه با زمان تخمینی و پیش نیاز آنها) در شکل زیر نشان داده شده است.

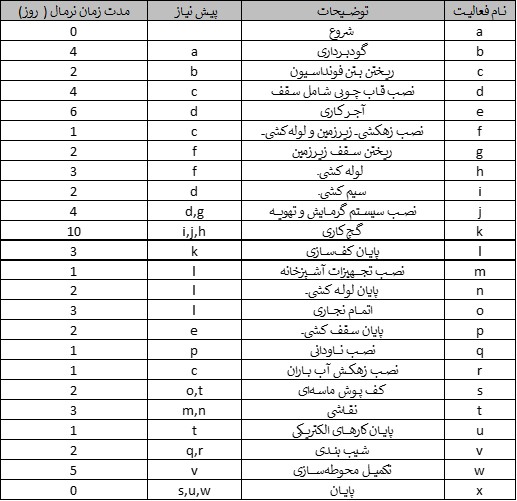
در این شکل ستون «پیش‌نیاز» توالی فعالیت‌ها را تعیین می‌کند و ما را قادر می‌سازد تا نمودار پروژه (شکل زیر) را ترسیم کنیم. در هر دایره حرف قبل از کاما، فعالیت را مشخص می‌کند و عدد بعد از کاما زمان فعالیت را نشان می‌دهد.

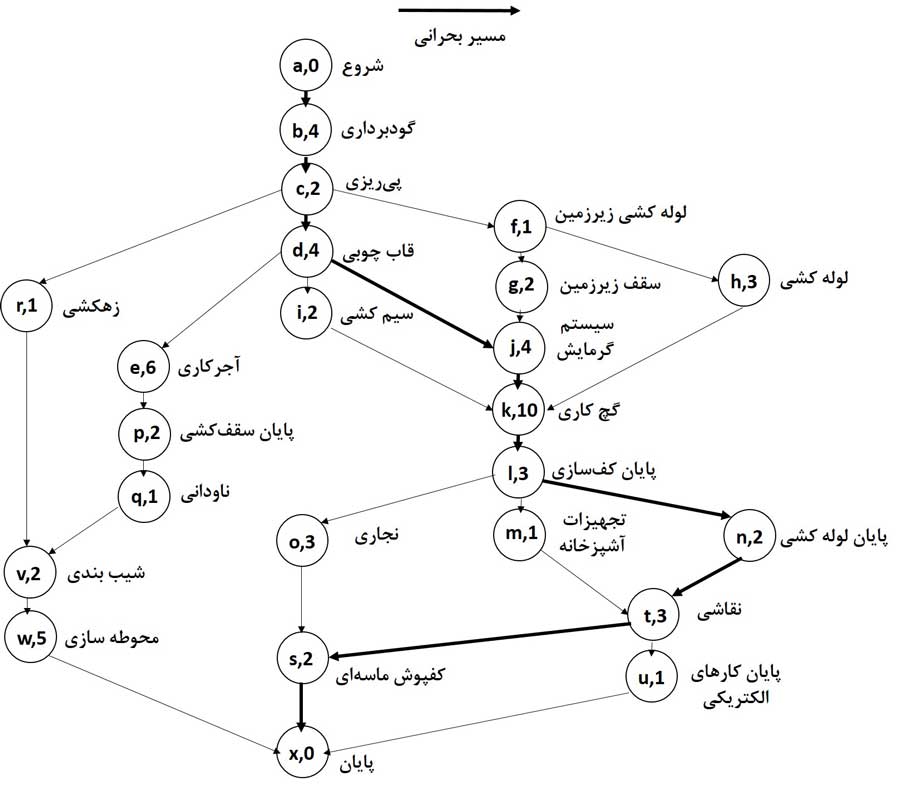
با حرکت در جهت فلش‌ها می‌توانیم ۲۲ مسیر منحصر به فرد را از شروع تا پایان، با حداقل زمان ۱۴ روز (مسیر abcrvwx) تا حداکثر زمان ۳۴ روز بشماریم (مسیر abcdjklntsx). دومین مسیر، بحرانی است. زمان کلی پروژه را تعیین می‌کند و به ما می‌گوید که کدام فعالیت‌ها از نظر تأثیرشان بر این زمان بحرانی هستند.

 اگر پیمانکار بخواهد خانه را در کمتر از ۳۴ روز تکمیل کند، کوتاه کردن فعالیت‌های خارج از مسیر بحرانی بی‌فایده است. مثلاً ممکن است به نظر او آجرکاری (e) پیشرفت را به تأخیر بیندازد، زیرا کار روی یک سری کار (p-q-v-w) باید منتظر بمانند تا e تکمیل شود. اما عجله در تکمیل آجرکاری بی‌نتیجه خواهد بود، زیرا در مسیر بحرانی قرار ندارد و بنابراین در تعیین زمان کل پروژه بی‌تاثیر است.

کوتاه کردن مسیر بحرانی

اگر پیمانکار از روش مسیر بحرانی (CPM) استفاده کند می‌تواند مسیر بحرانی را برای یافتن بهبودهای احتمالی بررسی کند. شاید بتواند نجارهای بیشتری را به فعالیت d اختصاص دهد و زمان آن را از ۴ روز به ۲ روز کاهش دهد. با این کار مسیر بحرانی کمی تغییر می‌کند و به جای d از کار f و g می‌گذرد. توجه داشته باشید که زمان کل پروژه فقط ۱ روز کاهش می‌یابد، حتی اگر ۲ روز از فعالیت d حذف شده باشد. بنابراین پیمانکار باید مراقب تغییر احتمالی مسیر بحرانی باشد زیرا ممکن است فعالیت‌های بحرانی را هم تغییر دهد.

کوتاه کردن مسیر بحرانی مستلزم در نظر گرفتن مشکلات مهندسی و مسائل اقتصادی است. آیا از نظر فیزیکی می‌توان زمان مورد نیاز فعالیت‌های بحرانی را کوتاه کرد (با اختصاص دادن افراد بیشتری به فعالیت، اضافه‌کاری، استفاده از تجهیزات مختلف و غیره)؟ اگر چنین است، آیا هزینه‌های افزایش سرعت کمتر از صرفه‌جویی ناشی از کاهش زمان کلی پروژه خواهد بود؟

روش مسیر بحرانی (CPM) ابزار مفیدی است زیرا:

• به سرعت توجه را بر روی فعالیت‌هایی متمرکز می‌کند که برای زمان پروژه بحرانی هستند و
• روشی آسان برای تعیین اثرات کوتاه کردن فعالیت‌های مختلف در پروژه ارائه می‌دهد.

مثالی از کاربرد روش مسیر بحرانی (CPM):

Du Pont، فردی که در کاربرد روش مسیر بحرانی (Critical Path Method) در پروژه‌های ساخت و ساز و تعمیر و نگهداری پیشگام بود، نگران مدت از کار افتادگی تجهیزات کارخانه‌های لوئیزویل در مدت تعمیر و نگهداری بود. این تجهیزات یک کالای واسطه را در فرآیند نئوپرن تولید می‌کردند. مهندسان Du Pont با تحلیل زمانبندی فرآیند تعمیر و نگهداری توسط روش مسیر بحرانی توانستند مدت از کار افتادگی برای تعمیرات را از ۱۲۵ به ۹۳ ساعت کاهش دهند. در نتیجه، عملکرد کارخانه حدود یک میلیون پوند در سال ۱۹۵۹ بهبود یافت.

با وجود این مزایا حتی در پروژه خانه‌سازی کوچک ما هم، روند شمارش و اندازه‌گیری طول هر مسیر خسته کننده است.

یک روش ساده برای یافتن مسیر بحرانی در ادامه توضیح داده شده است.

الگوریتم یافتن مسیر بحرانی در روش مسیر بحرانی (CPM)

۱)     یافتن زودترین زمانِ شروع و پایان

اگر زمان یا تاریخ شروع پروژه داده شده باشد (آن را با S نشان می‌دهیم)، برای هر فعالیت یک زودترین زمان شروع (ES) وجود دارد، که زودترین زمان ممکنی است که یک فعالیت در صورتی که تمام فعالیت‌های قبلی آن هم در زودترین زمانشان شروع شده باشند، می‌تواند شروع شود. اگر زمان تکمیل فعالیت t باشد، زودترین زمان پایان آن یعنی (EF) را ES + t تعریف می‌کنیم.

یک راه ساده برای محاسبه زمان‌های ES و EF با استفاده از نمودار پروژه وجود دارد:

• مقدار S را در سمت چپ و سمت راست Start بنویسید.
• در سمت چپ هر فعالیت جدیدی که همه پیش‌نیازهای آن مشخص شده‌اند، بیشترین عددی را که در سمت راست هر یک از پیش‌نیازهای آن قرار دارد، بنویسید. این عدد زمان شروع اولیه آن است.
• زمان فعالیت را به این عدد اضافه کنید و نتیجه (EF) را در سمت راست فعالیت بنویسید.
• ادامه دهید تا به Finish برسید.

در پایان این محاسبات، زمان ES برای هر فعالیت در سمت چپ دایره‌ای که آن را مشخص می‌کند، و زمان EF آن در سمت راست دایره ظاهر می‌شود. عددی که در سمت راست آخرین کار (پایان) ظاهر می‌‎شود، زودترین زمان پایان (F) برای کل پروژه است.

به طور خلاصه:

ES که زودترین زمان شروع هر فعالیت است در سمت چپ آن ظاهر شده و ماکزیمم اعداد سمت راست پیش نیازهایش است.

EF که دیرترین زمان پایان هر فعالیت است و در سمت راست هر فعالیت ظاهر می‌شود از ES+t  به دست می‌آید. (t زمان انجام هر فعالیت است.)

برای شفاف‌سازی این محاسبات، فرآیند تولید ساده زیر را در نظر بگیرید:

یک کالا باید از دو قطعه A و B ساخته شود. هر دو قطعه باید تراشکاری شوند و B باید جلا هم داده شود. (A نیازی به جلا ندارد.) فهرست فعالیت‌هایی که باید انجام شوند، همراه با پیش‌نیاز و زمان انجامشان بر حسب دقیقه، در شکل زیر آورده شده است.

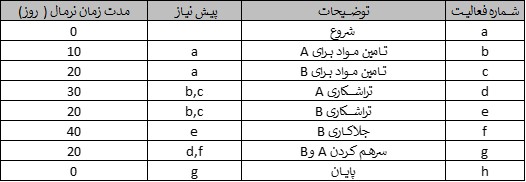
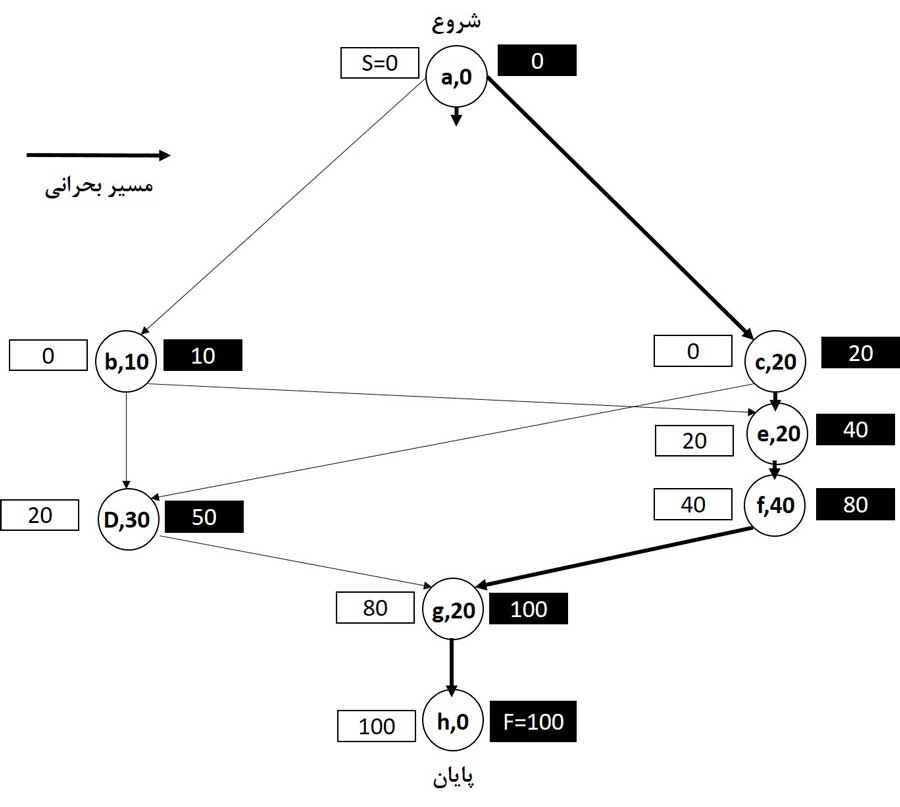
نمودار پروژه در شکل زیر نشان داده شده است. همانطور که قبلاً گفته شد، نام هر فعالیت قبل از کاما و زمان آن بعد از کاما ظاهر می‌شود. همچنین با فرض اینکه زمان شروع S صفر باشد، زمان‌های ES و EF برای هر فعالیت نشان داده شده است. زمان ES در سمت چپ دایره هر فعالیت و زمان EF در سمت راست آن ظاهر می‌شود. توجه داشته باشید که زودترین زمان پایان برابر ۱۰۰ است یعنی F = 100.

۲)     یافتن دیرترین زمانِ شروع و پایان

اکنون فرض کنید که یک زمان هدف (T) برای تکمیل پروژه داریم. واضح است که T باید بزرگتر یا مساوی F که زودترین زمان پایان پروژه است، باشد. با این فرض، می‌توانیم مفهوم دیرترین زمان پایان (LF) را تعریف کنیم. یعنی آخرین زمانی که یک فعالیت می‌تواند به پایان برسد، بدون اینکه باعث تاخیری بیش از زمان هدف پروژه (T) شود. به طور مشابه، دیرترین شروع (LS) به صورت LF-t تعریف می‌شود و t زمان انجام فعالیت است.

از انتهای پروژه قبلی به سمت ابتدای آن محاسبات را شروع می‌کنیم:

1. مقدار T را در سمت راست و چپ Finish بنویسید.
2. در سمت راست هر فعالیت جدیدی که همه فعالیت‌های پسین آن مشخص شده‌اند، کمترین عددی را که در سمت چپ هر یک از فعالیت‌های پسین آن قرار دارد یعنی کوچکترین LS فعالیت‌های پسین را بنویسید.
3. زمان فعالیت را از این عدد کم کنید و نتیجه را در سمت چپ بنویسید.
4. ادامه دهید تا به شروع برسید.

در پایان این محاسبه، زمان LF برای یک فعالیت در سمت راست دایره‌ای که آن را مشخص می‌کند، و زمان LS در سمت چپ دایره ظاهر می‌شود. عددی که در سمت راست Start ظاهر می‌شود، دیرترین زمانی است که کل پروژه می‌تواند شروع شود و همچنان در زمان هدف T پایان یابد.

در شکل زیر این محاسبات را برای مثال فرآیند تولید انجام دادیم. در اینجا T = F = 100 است و زودترین زمانِ شروع و پایان و دیرترین زمانِ شروع و پایان را با نقطه ویرگول جدا می‌کنیم. پس، ES ; LS در سمت چپ فعالیت و EF; LF  در سمت راست آن ظاهر می‌شود.

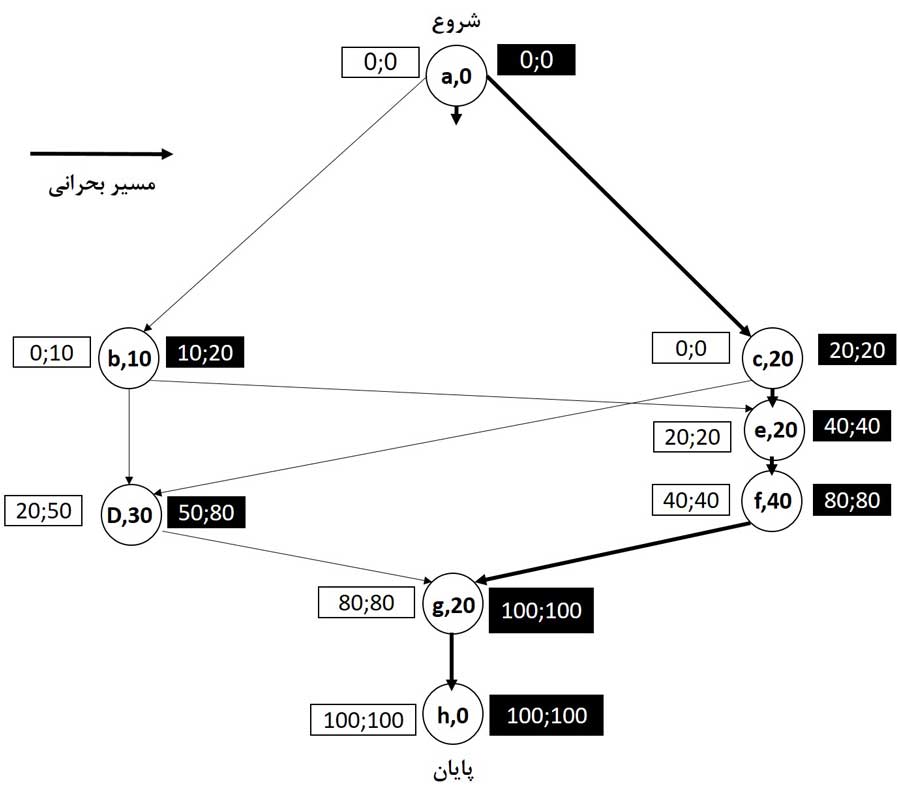
۳)     مفهوم شناوری (Slack)

بررسی شکل بالا نشان می‌دهد که زودترین زمان شروع برخی از فعالیت‌ها با دیرترین زمان شروعشان برابر است، در حالی که برخی دیگر اینطور نیستند. تفاوت بین زودترین و دیرترین زمان شروع یک فعالیت (یا بین زودترین و دیرترین زمان پایان آن) شناوری کل (TS) نامیده می‌شود. شناوری کل بیانگر حداکثر زمانی است که یک فعالیت ممکن است به تعویق بیفتد، بدون اینکه اتمام پروژه را به تاخیر بیندازد.

قبلاً فعالیت‌های بحرانی را فعالیت‎‌هایی در طولانی‌ترین مسیر پروژه تعریف کردیم. یعنی فعالیت‌های بحرانی به طور مستقیم بر زمان کلی پروژه تأثیر می‌گذارند. اکنون می‌توانیم مسیر بحرانی را به مفهوم شناوری مرتبط کنیم.

۴)     یافتن مسیر بحرانی

اگر تاریخ هدف (T) برابر با زودترین تاریخ اتمام کل پروژه (F) باشد، در این صورت همه فعالیت‌های بحرانی شناوری کلی برابر صفر دارند. به این معنی که تاریخ آنها ثابت و غیرقابل تغییر است. فعالیت‌های با شناوری مثبت در مسیر غیر بحرانی قرار دارند، به این معنی که ممکن است بدون تأثیر بر تاریخ اتمام پروژه، به تعویق بیفتند.

اگر T=F باشد همه فعالیت‌های بحرانی شناوری کلی برابر صفر دارند.

در شکل بالا، مسیر بحرانی با تیره کردن فلش‌هایی که فعالیت‌های بحرانی را به هم متصل می‌کنند، نشان داده شده است. در این نمونه فقط یک مسیر بحرانی وجود دارد و همه فعالیت‌های بحرانی در آن قرار دارند. با این حال، در موارد دیگر ممکن است بیش از یک مسیر بحرانی وجود داشته باشد. توجه داشته باشید که T = F؛ فعالیت‌های بحرانی دارای شناوری کلی صفر هستند. فعالیت b دارای TS = 10، و فعالیت d دارای TS = 30 است. یک یا هر دوی این فعالیت‌ها می‌توانند برابر TSشان به تعویق بیفتند بدون اینکه باعث تاخیر در کل پروژه شوند.

شناوری آزاد

نوع دیگری از شناوری قابل ذکر است. شناوری آزاد (FS) مقداری است که یک فعالیت می‌تواند بدون تاخیر در زودترین شروع هر فعالیت دیگری به تعویق بیفتد. یک فعالیت با شناوری کلی مثبت ممکن است شناوری آزاد داشته باشد و یا نداشته باشد. شناوری آزاد هرگز از شناوری کلی بیشتر نمی‌شود. برای مقاصد محاسباتی شناوری آزاد یک فعالیت، تفاوت بین زمان EF آن و کوچکترین ES همه فعالیت‌های پسین آن تعریف می‌شود.

کاربرد شناوری

هنگامی که یک فعالیت دارای شناوری کلی صفر است، زمان شروع برنامه‌ریزی شده آن ثابت است (یعنی ES = LS) و به تعویق افتادن زمان شروع محاسبه شده به معنای به تاخیر انداختن کل پروژه است. با این حال، کارهایی که دارای شناوری کلی مثبت هستند، به زمان‌بندی‌کننده اجازه می‌دهند تا در تنظیم زمان شروع کمی انعطاف‌پذیری داشته باشند. این انعطاف‌پذیری را می‌توان برای برنامه‌ریزی بهتر به کار برد.

به عنوان مثال می‌توان اوج بار کاری را با شیفت دادن فعالیت‌های روزهای اوج به دیرترین شروعشان کاهش داد. شناوری اجازه می‌دهد این کار بدون تأثیر بر زمان پروژه اتفاق بیفتد.

از شناوری آزاد می‌توان به طور موثر در سطح عملیاتی استفاده کرد. به عنوان مثال، اگر یک فعالیت دارای شناوری آزاد باشد، مدیر در تصمیم‌گیری برای شروع کار کمی انعطاف‌پذیری دارد. حتی اگر شروع کار را به میزان برابر یا کمتر از شناوری آزاد به تأخیر بیندازد، این تأخیر تاثیری بر زمان شروع یا شناوری فعالیت‌های بعدی نخواهد داشت (که این موضوع در مورد فعالیت‌های فاقد شناوری آزاد، صادق نیست). برای تشریح این مفاهیم، به مثال خانه‌سازی برمی‌گردیم.

درباره شناوری بیشتر بخوانید.

بازگشت به مثال خانه‌سازی برای محاسبات روش مسیر بحرانی (Critical Path Method)

باید بدانید که اگر T بزرگتر از F باشد، آنگاه فعالیت‌های بحرانی شناوری کلی برابر با T-F خواهند داشت که مقدار حداقل شناوری است. از آنجایی که مسیر بحرانی فقط فعالیت‌های بحرانی را شامل می‌شود، پس همه فعالیت‌های این مسیر دارای حداقل شناوری کل هستند. همه فعالیت‌های غیر بحرانی شناوری کل بیشتری خواهند داشت.

در شکل زیر نمودار فعالیت‌های خانه‌سازی را بازتولید می‌کنیم، ES و LS را در سمت چپ و EF و LF را در سمت راست هر فعالیت می‌نویسیم (برای مثال، ۳;۰ و ۷;۴ در دو طرف b,4). فرض می‌کنیم که ساخت و ساز در روز صفر شروع می‌شود و باید تا روز ۳۷ تکمیل شود. شناوری کل برای هر فعالیت مشخص نشده، زیرا واضح است که تفاوت بین اعداد ES و LS یا EF و LF است. با این حال، فعالیت‌هایی که دارای شناوری آزاد مثبت هستند، مشخص شده‌اند. یک مسیر بحرانی وجود دارد که در نمودار نشان داده شده است. تمام فعالیت‌های بحرانی در این مسیر دارای شناوری کلی سه روز هستند.

اگر T>F باشد همه فعالیت‌های بحرانی حداقل شناوری کل را بین فعالیت‌ها دارند و مقدار این شناوری T-F است.

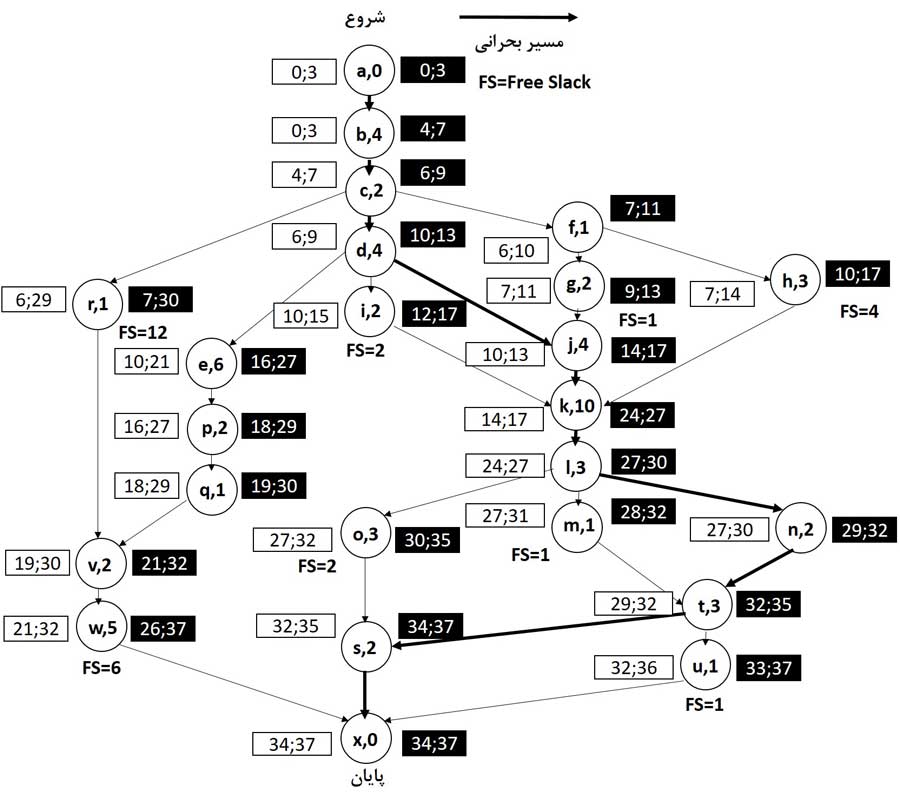
با مشاهده نمودار به اطلاعات زیر می‌رسیم:

• در صورت عدم رخداد مشکلات پیش‌بینی نشده، پیمانکار می‌تواند شروع به کار را ۳ روز به تعویق بیندازد و همچنان آن را طبق زمابندی کامل کند. (تفاوت بین زودترین و دیرترین زمان‌ها را در پایان ببینید). این باعث می‌شود سه روز از شناوری کلی همه فعالیت‌ها کاسته شود و بنابراین TS برای فعالیت‌های بحرانی به صفر برسد.
• بسیاری از فعالیت‌ها دارای شناوری آزاد هستند. بنابراین پیمانکار می‌تواند تکمیل i را ۲ روز، g را ۱ روز، h را ۴ روز، r را ۱۲ روز به تاخیر بیاندازد، (و موارد دیگر) بدون اینکه بر فعالیت‌های بعدی تأثیر بگذارد.
• فعالیت‌های e، p، q،v و w دارای میزان شناوری کلی (۹ روز) هستند. پیمانکار می‌‎تواند از این فعالیت‌ها به عنوان فعالیت‌های “پر کننده” برای کارگران در مواقعی که مهارت‌های آنها برای فعالیت‌های بحرانی ضروری نیست، استفاده کند. با دستکاری فعالیت‌های دارای شناوری اوج تقاضا برای کارگران یا تجهیزات خاص کاهش داده می‌شود.

محاسبه مسیر بحرانی با نرم افزار مدیریت پروژه

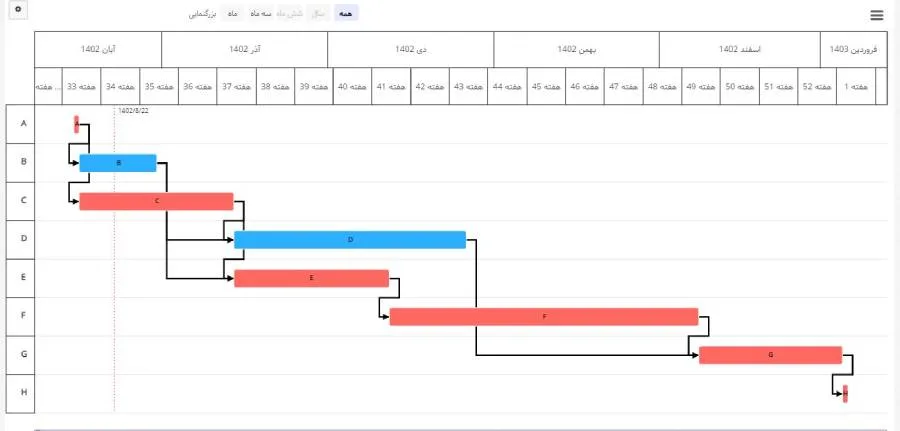
محاسبه مسیر بحرانی برای فعالیت‌ها می‌تواند بسیار ارزشمند باشد، اما انجام محاسبات به صورت دستی برای بیشتر پروژه‌ها به دلیل پیچیدگی آنها غیرممکن است. استفاده از ابزارهای مدیریت پروژه مانند بهتایم راهکار مناسبی است. این نرم افزارها محاسبات مسیر بحرانی را انجام داده و نتیجه را در اختیار شما قرار می‌دهند. به عنوان مثال برای محاسبه مسیر بحرانی در بهتایم کافیست مراحل زیر را انجام دهید:

1. پروژه را در بهتایم تعریف کنید. (مشاهده آموزش تعریف پروژه)
2. فعالیت‌های پروژه را تعریف کنید و یا آنها را به بهتایم وارد کنید. (تاریخ شروع و سررسید فعالیت‌ها را مشخص کنید.)
3. به گانت چارت پروژه مراجعه کنید و روابط پیش‌نیازی را با چند کلیک ساده برقرار کنید.
4. پس از این مرحله، بهتایم مسیر بحرانی را با قرمز کردن فعالیت‌های روی آن به شما نمایش می‌دهد.

نتیجه مقاله الفبای روش مسیر بحرانی (Critical Path Method)

برای مدیران پروژه CPM یک ابزار قدرتمند و انعطاف‌پذیر برای تصمیم‌گیری است:

• در مراحل مختلف مدیریت پروژه، از برنامه‌ریزی اولیه یا تحلیل برنامه‌‎های جایگزین گرفته تا زمان‌بندی و کنترل فعالیت‌هایی که یک پروژه را تشکیل می‌دهند، مفید است.

• می‌توان آن را در انواع مختلفی از پروژه‌ها به کار برد.

• به روشی ساده و مستقیم، روابط متقابل مجموعه فعالیت‌هایی که یک پروژه بزرگ را تشکیل می‌دهند، نشان می‌دهد.

• این روش با استفاده از نمودار پروژه به راحتی برای افراد غیر متخصص قابل توضیح است. محاسبات داده‌ها برای پروژه‌های بزرگ به راحتی می‌توانند توسط رایانه انجام شوند.

• مجموعه فعالیت‌هایی را که برای زمان اتمام پروژه حیاتی هستند، مشخص می‌کند، بنابراین به برنامه‌ریزی و کنترل دقیق‌تر کمک می‌کند.

• به مدیر امکان می‌دهد تا گلوگاه‌های بالقوه‌ای را که ممکن است از کوتاه کردن فعالیت‌های حیاتی ناشی شوند، پیش‌بینی کند.

• منجر به تخمین معقولی از هزینه‌های پروژه برای تاریخ‌های تکمیل مختلف می‌شود و مدیر را قادر می‌سازد تا زمان‌بندی بهینه را انتخاب کند.

مدیریت پروژه آسان با نرم افزار مدیریت پروژه آنلاین بهتایم

مراجع:

• https://hbr.org
• https://asana.com