تحلیل GERT در مدیریت پروژه چیست؟

استفاده از تحلیل شبکه در برنامه‌ریزی و کنترل پروژه از اواخر دهه ۱۹۵۰ گسترده شده است، PERT و CPM، از بهترین تکنیک‌های مدل‌سازی شبکه هستند که در پروژه‌های متنوعی برای اهداف برنامه‌‌ریزی و کنترل پروژه به کار گرفته می‌شوند. با این حال، PERT و CPM دارای محدودیت‌هایی هستند که مدل‌سازی بسیاری از پروژه‌های پیچیده را غیرممکن می‌کنند. یک ابزار شبکه انعطاف‌پذیرتر که اخیراً مورد توجه قرار گرفته، تحلیل GERT است.

Graphical Evaluation and Review Technique = تحلیل GERT

تخمین مدت زمان انجام فعالیت‌های پروژه، بخش مهمی از هر فرآیند برنامه‌ریزی پروژه را تشکیل می‌دهد. هنگامی که فعالیت‌هایی را که باید انجام دهید تا نیازهای مشتری خود را با موفقیت برآورده کنید، می‌شناسید، باید تعیین کنید که هر فعالیت چقدر طول می‌کشد و یک برنامه پروژه ایجاد کنید.

این پست تکنیک ارزیابی و بازبینی گرافیکی (تحلیل GERT) را معرفی می‌کند که ابزاری قابل اعتماد برای ایجاد تخمین‌های دقیق برای مدت زمان فعالیت است.

تکنیک ارزیابی و بررسی گرافیکی (تحلیل GERT) چیست؟

شبکه‌های PERT/CPM به طور کلی شناخته‌‎تر هستند. با این حال، از آنجایی که شبکه‌های GERT از نظر ساختار شبیه به شبکه‌های PERT/CPM هستند، مرور مختصر عناصر PERT/CPM مفید خواهد بود.

• درباره PERT بیشتر بخوانید.
• درباره CPM بیشتر بخوانید.

شبکه‌های PERT/CPM از دو جزء اصلی، فعالیت‌ها و رویدادها تشکیل شده‌اند. فعالیت‌های شبکه با گره و رویدادها که در واقع توالی فعالیت‌ها هستند با فلش نشان داده می‌شوند. PERT و CPM از این جهت متفاوت هستند که در فعالیت‌های CPM تنها یک عدد ثابت برای مدت زمان فعالیت‌ها در نظر گرفته می‌شوند، در حالی که در PERT زمان‌ فعالیت‌ها احتمالی هستند و از فرمول تخمین زیر برای آنها استفاده می‌شود:

 (O + (4 × M) + P)/6

• برآورد زمانی خوش‌بینانه: o
• برآورد زمانی محتمل: M
• برآورد زمانی بدبینانه : P

عناصر یک نمودار تحلیل GERT

 ۱. گره‌ها (رویدادها):

گره‌های انتهایی: شروع یا پایان فرآیند را نشان می‌دهند.

گره‌های غیرانتهایی: نمایانگر رویدادها یا نقاط عطف میانی پروژه هستند.

گره‌ها با کمان‌ها به هم متصل می‌شوند تا ترتیب فعالیت‌ها و تصمیمات را نشان دهند.

۲. کمان‌ها (فعالیت‌ها و شاخه‌ها):

کمان‌های قطعی: فعالیت‌هایی با نتایج ثابت و مدت زمان مشخص.

کمان‌های احتمالی: فعالیت‌ها یا رویدادهایی با نتایج نامشخص که معمولاً با احتمالات همراه هستند.

کمان‌ها می‌توانند شامل اطلاعاتی درباره زمان، هزینه و توزیع احتمالات باشند تا نمایی دقیق‌تر از مسیر پروژه ارائه دهند.

۳. عملگرهای منطقی:

AND: به اتمام همه فعالیت‌های ورودی، قبل از پیشروی به گره بعدی، نیازمند است.

OR: اجازه می‌دهد که فرآیند با اتمام هر یک از فعالیت‌های ورودی ادامه یابد.

۴. احتمالات:

هر کمان احتمالی دارای احتمالی است که نشان‌دهنده احتمال انتخاب آن مسیر است.

احتمالات به ارزیابی سناریوها و نتایج مختلف کمک می‌کنند و برنامه‌ریزی انعطاف‌پذیر و واقع‌گرایانه‌تری را امکان‌پذیر می‌سازند.

۵. لوپ‌ها:

برخلاف روش‌های PERT و GERT ،CPM اجازه می‌دهد که در شبکه لوپ وجود داشته باشند، به این معنی که فعالیت‌ها می‌توانند بر اساس شرایط یا نتایج خاصی چندین بار تکرار شوند.

لوپ‌ها به مدل‌سازی فرآیندهای تکراری و حلقه‌های بازخورد کمک می‌کنند که معمولاً در پروژه‌های تحقیق و توسعه یافت می‌شوند.

۶. توزیع‌ها:

مدت زمان و هزینه فعالیت‌ها می‌توانند از توزیع‌های احتمالی مختلفی (مثلاً توزیع نرمال، بتا، یا نمایی) پیروی کنند که امکان مدل‌سازی دقیق‌ترِ عدم قطعیت‌های دنیای واقعی را فراهم می‌کنند.

برای ترسیم یک شبکه تحلیل GERT، مراحل زیر را دنبال کنید:

 تعریف فعالیت‌های پروژه:

• تمام فعالیت‌ها و رویدادهای پروژه را فهرست کنید.
• مشخص کنید کدام فعالیت‌ها قطعی هستند (نتایج و مدت زمان ثابت) و کدام‌ احتمالی (نتایج و مدت‌های متغیر).

 گره‌ها را شناسایی کنید:

• گره‌های شروع و پایان پروژه را تعیین کنید.
• گره‌های میانی (رویدادها) را که نشان دهنده نقاط عطف مهم یا نقاط تصمیم‌گیری در پروژه هستند، شناسایی کنید.

وابستگی‌ها را تعیین کنید:

• توالی منطقی فعالیت‌ها را تعیین کنید.
• تعریف کنید که فعالیت‌ها چگونه به هم مرتبط هستند و برای حرکت از یک فعالیت به فعالیت دیگر چه شرایطی باید رعایت شود.

 گره‌ها و کمان‌ها را رسم کنید:

• گره‌ها: با دایره یا مستطیل نشان داده می‌شوند.

 گره شروع: شروع پروژه را نشان می‌دهد.

 گره اتمام: نشان‌دهنده اتمام پروژه است.

 گره‌های میانی: نشان‌دهنده نقاط تصمیم‌گیری یا نقاط عطف هستند.

• کمان‌ها: خطوط جهت‌داری که گره‌ها را به هم متصل می‌کنند.

 فلش‌ها: جهت گردش کار را نشان می‌دهند.

 هر کمان را با نام فعالیت، مدت زمان و احتمال (در صورت وجود) نام‌گذاری کنید.

 عملگرهای منطقی را اضافه کنید:

 AND: از این عملگرها برای نشان دادن اینکه چندین فعالیت باید قبل از حرکت به گره بعدی تکمیل شوند، استفاده کنید. اغلب با یک دایره یا نقطه کوچک نشان داده می‌شوند.

 OR: از این عملگرها برای نشان دادن اینکه هر یک از فعالیت‌های ورودی اجازه پیشرفت به گره بعدی را می‌دهد، استفاده کنید. آنها را می‌توان مشابه با دروازه‌های AND نشان داد اما برای نشان دادن تفاوتشان آنها را برچسب‌گذاری کنید.

احتمالات و مدت زمان را تخصیص دهید:

• برای کمان‌های احتمالی، احتمال هر مسیر را مشخص کنید.
• مدت زمان هر فعالیت را مشخص کنید. اگر مدت زمان نامشخص است، از توزیع احتمال برای نمایش آنها استفاده کنید.

 لوپ‌ها را قرار دهید:

• اگر پروژه شامل فرآیندهای تکراری است، لوپ‌ها را در شبکه GERT خود قرار دهید.
• از کمان‌های بازخورد برای نمایش فعالیت‌هایی که ممکن است بر اساس شرایط یا نتایج خاصی تکرار شوند، استفاده کنید.

مثالی برای ترسیم شبکه تحلیل GERT

گام ۱: تعریف فعالیت‌های پروژه و شناسایی وابستگی‌ها

• وظیفه A (شروع پروژه)
• وظیفه B (بعد از وظیفه A، با ۵۰% احتمال نیاز به بازگشت به وظیفه A)
• وظیفه C (بعد از وظیفه B)
• وظیفه D (بعد از وظیفه A و به صورت موازی با وظایف B و C)
• وظیفه E (بعد از وظایف C و D، پایان پروژه)

گام ۲: تعریف گره‌ها و لوپ‌‌ها

• گره ۱: شروع
• گره ۲: پایان وظیفه A
• گره ۳: پایان وظیفه B
• گره ۴: پایان وظیفه C
• گره ۵: پایان وظیفه D
• گره ۶: پایان وظیفه E (پایان پروژه)

• A: ۱→۲
• B: ۲→۳
• C: ۳→۴
• D: ۲→۵
• E: ۴,۵→۶

وظیفه B دارای ۵۰% احتمال بازگشت به وظیفه A است، که به صورت ۲→۲ نمایش داده می‌شود.

گام ۳: رسم نمودار شبکه

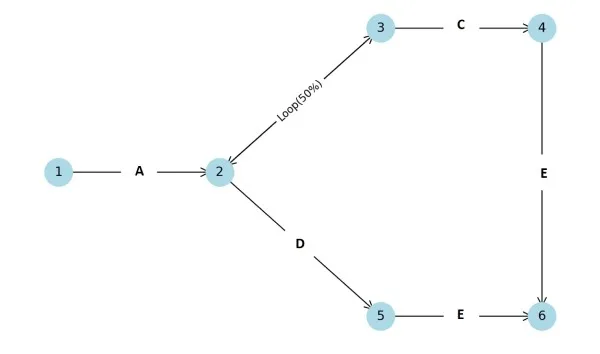
 گام ۴: اختصاص دادن احتمالات و مدت زمان‌ها

مدت زمان هر وظیفه به شرح زیر است: (برحسب روز)

• A: 3
• B: 4
• C: 2
• D: 3
• E: 5

احتمال هر وظیفه:

• A: 100% (1.0)
• احتمال موفقیت ۵۰% و احتمال بازگشت B: 50%
• C: 100% (1.0)
• D: 100% (1.0)
• E: 100% (1.0)

مدت زمان مورد انتظار هر فعالیت را با استفاده از فرمول زیر محاسبه کنید:

{مدت زمان مورد انتظار} = {احتمال}  X {مدت زمان}

• A: 3
• C: 2
• D: 3
• E: 5

محاسبه لوپ برای B:

 در روش GERT، برای محاسبه تعداد انتظار تکرارها برای یک وظیفه که احتمال بازگشت دارد، از فرمول زیر استفاده می‌شود:

E(N)=k=∑_۱^∞​ (K.P)

P احتمال دقیقاً k بار تکرار شدن وظیفه B است.

وظیفه B با احتمال ۵۰% نیاز به بازگشت دارد.

با توجه به اینکه هر بار احتمال بازگشت ۵۰% (یا ۰.۵) است:

برای k=1: احتمال اینکه وظیفه B فقط یک بار انجام شود (بدون بازگشت) برابر است با ۰.۵.

k=2: احتمال اینکه وظیفه B دو بار انجام شود (یک بار انجام و یک بار بازگشت) برابر است با ۰.۵×۰.۵=۰.۲۵

k=3: احتمال اینکه وظیفه B سه بار انجام شود (دو بار بازگشت) برابر است با ۰.۵×۰.۵×۰.۵=۰.۱۲۵

و به همین ترتیب ادامه دارد.

محاسبه E(N) که یک سری هندسی است که به صورت زیر می‌توان آن را ساده کرد:

E(N)=1⋅۰.۵+۲⋅(۰.۵)^۲+۳⋅(۰.۵)^۳+…

سری هندسی بالا به صورت زیر ساده می‌شود:

E(N)=0.5+0.5^۲+۰.۵^۳+…=۱

اما چون هر بار k در مقدار خودش ضرب شده است، نتیجه نهایی برابر خواهد بود با:

E(N)=1+0.5+0.25+0.125+…=۲

نتیجه:

E(N)=2

بنابراین، تعداد انتظار تکرارها برای وظیفه B با توجه به احتمال ۵۰% بازگشت، برابر با ۲ است. این به این معنی است که به طور میانگین، وظیفه B دو بار انجام می‌شود تا نهایتاً بدون بازگشت به گره بعدی برود.

گام ۵: محاسبه مدت زمان‌های مورد انتظار

مدت زمان انتظار برای وظیفه B:

E(D)=2 ×۴ =۸ (روز)

مدت زمان مورد انتظار کلی:

مسیر ۱ (A → B → C → E):

۳+۸+۲+۵=۱۸ روز

مسیر ۲ (A → D → E):

۳+۳+۵=۱۱ روز

مدت زمان مورد انتظار کلی (با توجه به محتمل‌ترین مسیر):

چون هر دو مسیر باید تکمیل شوند تا پروژه به پایان برسد، مدت زمان مورد انتظار حداکثر زمان هر دو مسیر است.

max⁡(۱۸,۱۱)=۱۸ روز

گام ۶: رسم نمودار تحلیل GERT

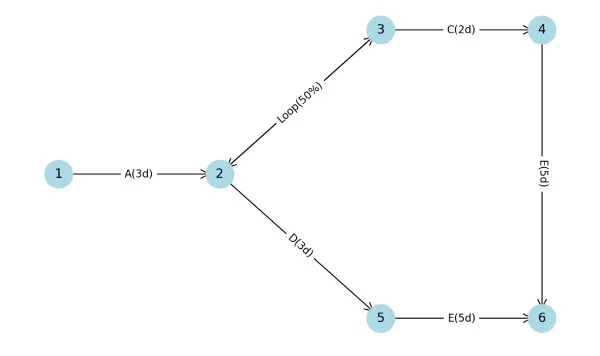
با پیروی از این مراحل، می‌توانید نمودار GERT را برای هر پروژه‌ای ایجاد کنید و طبیعت احتمالی فعالیت‌ها و مدت زمان آن‌ها را در نظر بگیرید که نمایی واقع‌گرایانه‌تر از پروژه‌های پیچیده نسبت به روش‌های سنتی فراهم می‌کند.

در کشیدن نمودار تحلیل GERT به موارد زیر توجه کنید:

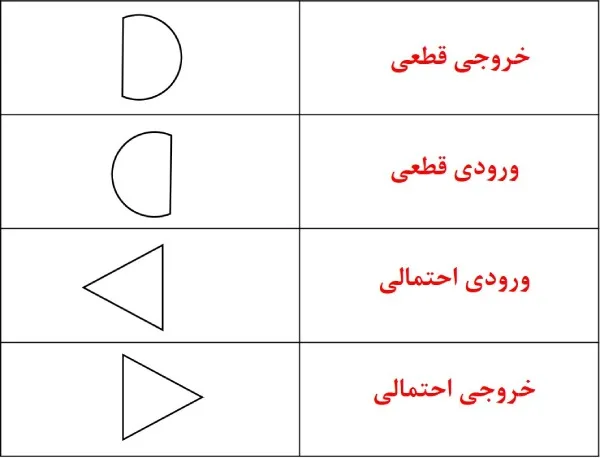
مزایا و معایب تحلیل GERT در مدیریت پروژه

مزایای تحلیل GERT

• مدیریت عدم قطعیت

 GERT امکان درج گره‌های احتمالی و لوپ‌ها را در یک شبکه پروژه فراهم می‌کند که به مدیران پروژه کمک می‌کند تا عدم قطعیت‌های ذاتی در پروژه‌های پیچیده را به طور مؤثر مدیریت کنند و نمایش دهند.

• انعطاف‌پذیری

GERT رویکردی انعطاف‌پذیر در مدل‌سازی پروژه ارائه می‌دهد. برخلاف تکنیک‌های سنتی مدیریت پروژه که از مسیرها و فعالیت‌های ثابت استفاده می‌کنند، GERT امکان مدل‌سازی نتایج و مسیرهای مختلف را فراهم می‌کند و تغییرات و تکرارها را در طول پروژه می‌پذیرد.

• ساده‌سازی پروژه‌های پیچیده

با تجزیه پروژه‌های پیچیده به شبکه‌ای ساده‌تر از فعالیت‌های وابسته به هم، GERT به مدیران پروژه کمک می‌کند تا برنامه‌ریزی و مدیریت پروژه را به صورت مؤثرتری انجام دهند.

• ارتقای ارتباطات

GERT به عنوان ابزاری قابل اعتماد برای ارتباط بین ذینفعان مختلف پروژه عمل می‌کند زیرا نمایشی شفاف و قابل مشاهده از وظایف و وابستگی‌های پروژه ارائه می‌دهد.

معایب تحلیل GERT

• پیچیدگی در مدل‌سازی

ایجاد و تحلیل نمودارهای GERT می‌تواند پیچیده و چالش‌برانگیز باشد. استفاده از گره‌های احتمالی و لوپ‌ها نیاز به دانش پیشرفته‌ای از روش‌های آماری دارد که می‌تواند برای برخی از مدیران و تیم‌های پروژه مانع باشد.

• آشنایی محدود

GERT هنوز در حوزه مدیریت پروژه نسبتاً جدید است و بسیاری از تیم‌ها هنوز در حال یادگیری چگونگی استفاده کامل از قابلیت‌ها و بهره‌برداری از مزایای آن هستند.

• مصرف منابع

مدل‌سازی و تحلیل دقیق در GERT می‌تواند از نظر زمان و تلاشی که برای آن صرف می‌شود، منابع‌بر باشد. توسعه نمودارهای دقیق GERT و انجام شبیه‌سازی‌ها نیاز به سرمایه‌گذاری قابل توجهی در آموزش و منابع محاسباتی دارد.

تفاوت‌های تحلیل PERT و تحلیل GERT

PERT (تکنیک ارزیابی و مرور برنامه) و GERT (تکنیک ارزیابی و مرور گرافیکی) دو روش مختلف برای مدیریت پروژه‌ها هستند که هر یک دارای ویژگی‌ها، مزایا و کاربردهای خاص خود هستند. در ادامه به تفاوت‌های اصلی بین این دو روش پرداخته می‌شود:

۱. مدل‌سازی و انعطاف‌پذیری

PERT:

• ساختار خطی: PERT یک روش زمان‌بندی خطی است که از نمودارهای شبکه‌ای برای نمایش فعالیت‌های پروژه استفاده می‌کند. در این نمودارها، هر فعالیت به صورت دنباله‌ای از مراحل که به صورت ترتیبی انجام می‌شوند، نمایش داده می‌شود.
• عدم حمایت از لوپ‌ها و گره‌های احتمالی: PERT نمی‌تواند عدم قطعیت‌های پروژه را با استفاده از لوپ‌ها و گره‌های احتمالی مدل‌سازی کند. هر فعالیت باید دقیقاً یک مسیر و زمان‌بندی مشخص داشته باشد.

تحلیل GERT:

• مدل‌سازی احتمالی: GERT از نمودارهای احتمالی استفاده می‌کند که به مدیران پروژه اجازه می‌دهد تا عدم قطعیت‌های موجود در پروژه را با استفاده از گره‌های احتمالی و لوپ‌ها مدل‌سازی کنند. این امکان باعث می‌شود که GERT بتواند شرایط مختلف و نتایج محتمل را در نظر بگیرد.
• حلقه‌ها و بازخوردها: در GERT، امکان ایجاد لوپ‌ها و بازخوردها وجود دارد که به پروژه‌ها اجازه می‌دهد تا مسیرهای مختلف را تکرار کنند و مجدداً بررسی شوند.

۲. کاربردها و پیچیدگی

PERT:

• تمرکز بر زمان‌بندی: PERT عمدتاً برای برنامه‌ریزی و زمان‌بندی پروژه‌ها استفاده می‌شود و بر اساس شناسایی و تحلیل مسیر بحرانی (Critical Path) عمل می‌کند. این تکنیک به پیش‌بینی زمان مورد نیاز برای تکمیل پروژه‌ها کمک می‌کند.
• سادگی نسبی: PERT نسبت به GERT ساده‌تر است و نیاز به ابزار و دانش‌ پیچیده‌ای ندارد. این روش بیشتر در پروژه‌های با پیچیدگی کمتر و زمان‌بندی خطی استفاده می‌شود.

تحلیل GERT:

• مدل‌سازی پیچیده: GERT به دلیل نیاز به شبیه‌سازی‌های پیچیده، مانند شبیه‌سازی مونت کارلو، می‌تواند پیچیده و زمان‌بر باشد و نیاز به دانش و مهارت‌های خاصی دارد.
• استفاده در پروژه‌های پیچیده: GERT برای پروژه‌های پیچیده‌تر که دارای عدم قطعیت‌های زیاد و مسیرهای مختلف هستند، مناسب‌تر است.

۳. نمودارها و نمایش

PERT:

• نمودار شبکه‌ای: نمودارهای PERT به صورت شبکه‌ای نمایش داده می‌شوند که شامل فعالیت‌ها و روابط زمانی بین آنها هستند. هر فعالیت به صورت یک گره در شبکه نمایش داده می‌شود و ارتباطات بین آنها به صورت فلش نشان داده می‌شود.
• سه زمان برای هر فعالیت: در PERT، هر فعالیت به سه زمان مختلف (خوش‌بینانه، بدبینانه و محتمل) زمان‌بندی می‌شود تا میانگین زمانی برای تکمیل هر فعالیت محاسبه شود.

تحلیل GERT:

• نمودارهای احتمالی: نمودارهای GERT به صورت شبکه‌های احتمالی نمایش داده می‌شوند که شامل گره‌های احتمالی و لوپ‌ها هستند. این نمودارها به مدیران پروژه اجازه می‌دهند تا مسیرهای مختلف و شرایط احتمالی را نمایش دهند.
• شبیه‌سازی مونت کارلو: برای مدل‌سازی و تحلیل دقیق شبکه‌های GERT، اغلب به شبیه‌سازی مونت کارلو نیاز است که به پیش‌بینی نتایج مختلف کمک می‌کند.

ساده‌ترین تکنیک مدیریت پروژه، روش مسیر بحرانی است که البته نرم افزار مدیریت پروژه بهتایم به سادگی مسیر بحرانی را برای شما محاسبه کرده و نمایش می‌دهد، در آدرس زیر می‌توانید به رایگان آن را تست کنید:

ثبت نام رایگان در بهتایم

مراجع:

• https://www.pmi.org
• https://aprika.com
• https://www.rand.org